◄Back

三维网格模型的重采样与网格重建

---

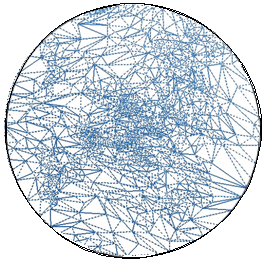
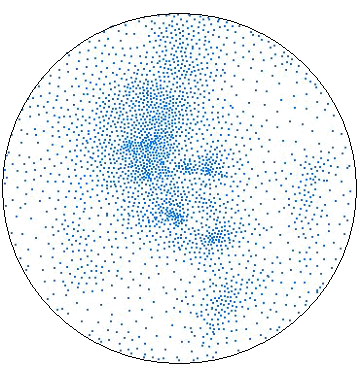
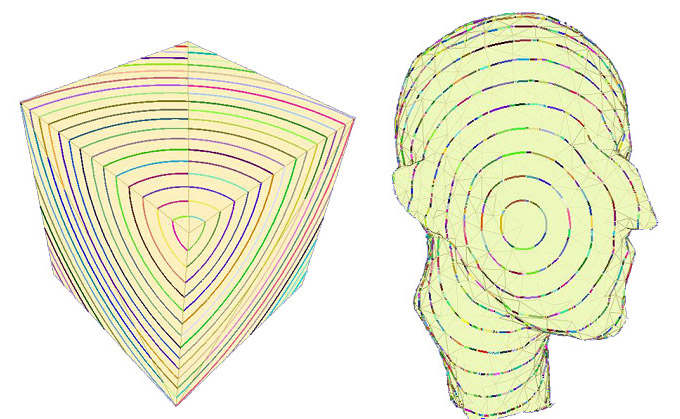
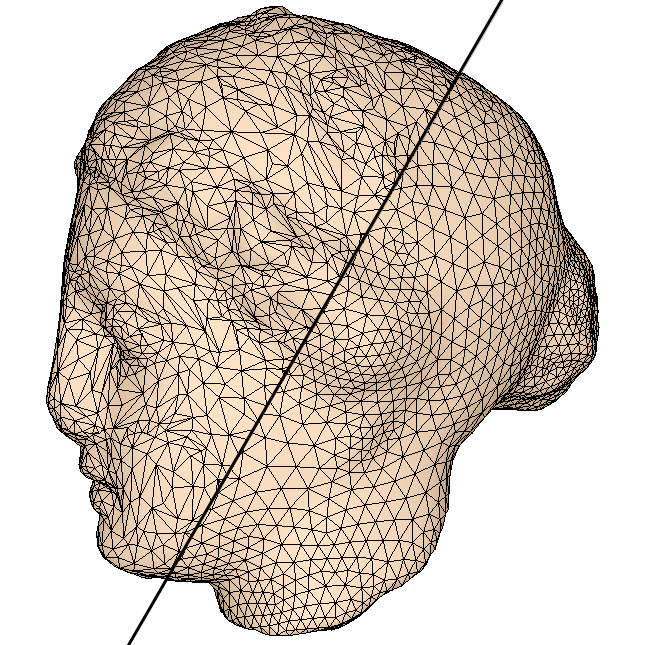
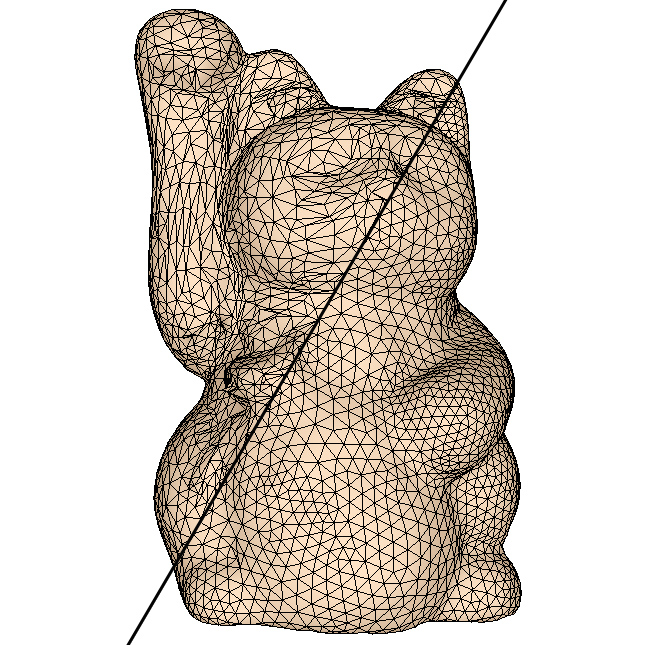
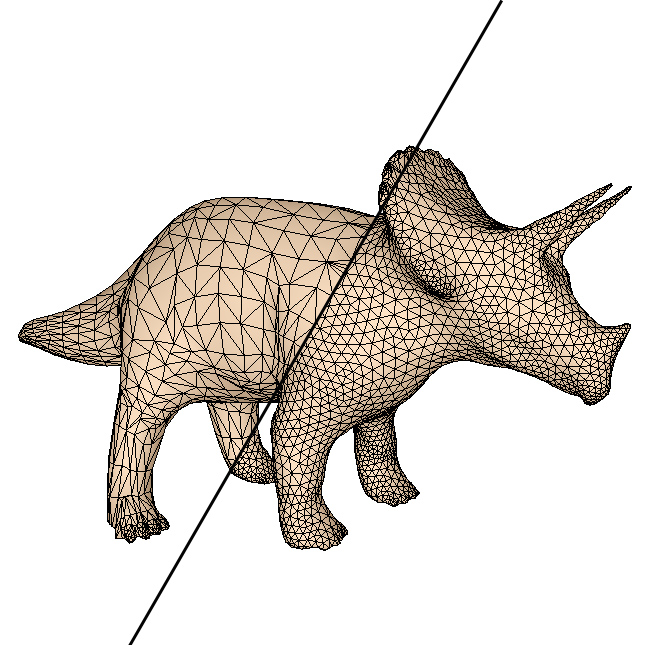
针对多边形网格模型数据量大、不便于编辑传输等问题，本课题的主要研究目的就是通过采样和重建对三维流形网格模型进行调整，对多边形的数量和形状进行优化，从而提高模型的质量和处理速度。为此我们需要对三角网格模型的顶点进行重采样，使新的顶点集合符合一定的密度函数，并具有较好的分布性质。在此基础上重新进行三角化，可以得到质量更高的优化三角网格模型。

要通过模型本身的性质来控制顶点分布密度，就需要研究三维流形表面上的采样技术。通过将三维模型转化到二维空间对其进行重要性采样来控制顶点的数量和分布，再进行网格重建是一种快速而有效的方法。本课题中首先研究了通过优化切割和保角映射对三维网格模型进行二维参数化的方法。为了将任意封闭网格模型参数化到平面域中，我们先找到一个最优化的切线集将模型切割成一个或若干个与圆盘同胚的区域，然后对每个区域进行二维参数化。而后，在参数空间中应用较为成熟的二维采样算法（如二维误差扩散采样算法）进行重采样，再将采样结果重新映射回三维模型表面。利用这种方法我们实现了三维模型表面上的自适应的重要性采样方法，其中采样密度分布可控，并且每个局部区域内的采样点都能满足蓝噪声性质。自适应采样算法可以根据三维表面上的曲率等几何信息调制采样密度函数，使样点分布与三维几何特征更为吻合，得到更好的采样点集。

　

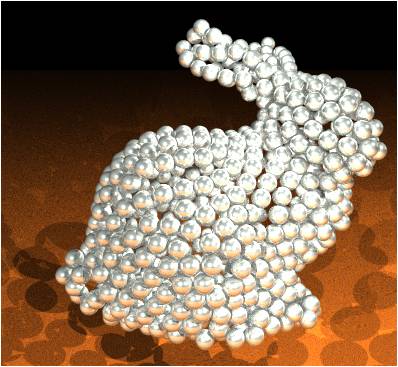
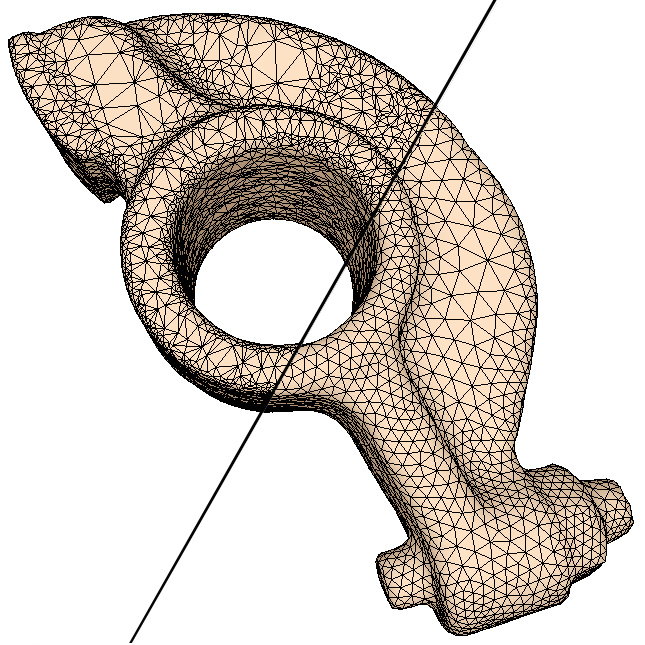
另一方面，我们也可以将二维空间中的采样算法（如泊松圆盘采样算法）扩展到三维空间中，这样对于一些不可展开的模型，可以避免参数化引入的扭曲。在三维空间中，我们采用了最短测地路径作为三维网格表面的距离度量，可以计算出三维网格表面上的可用边界，从而将泊松圆盘采样算法扩展到三维流形表面上。在此基础上，结合现有的GPU并行计算新技术，我们还提出了一种三维表面上的并行泊松圆盘采样算法。该算法在三维流形表面上进行三角形分组聚类，并利用GPU对不同分组进行并行的采样计算。从实验结果可以看出，本项目的三维表面并行采样算法能够在保证采样点的蓝噪声性质的同时大大提高采样的效率。

▲ 利用三维表面重采样结果进行纹理映射和物体分布的结果

　

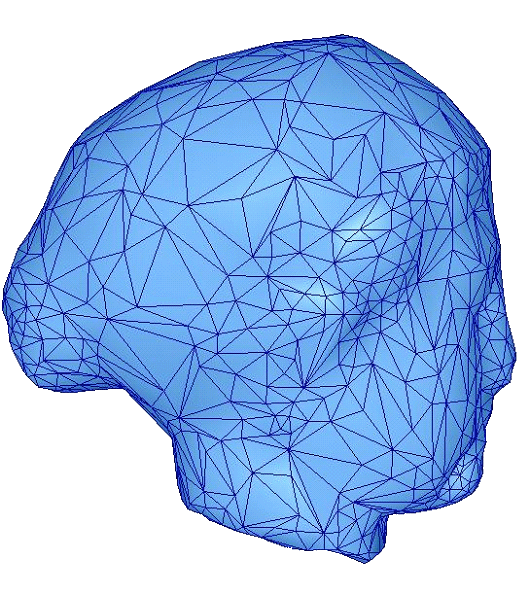
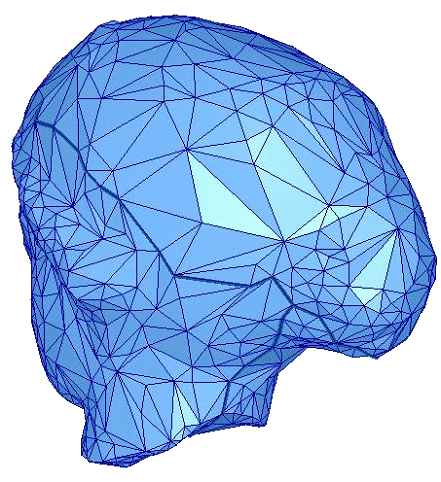
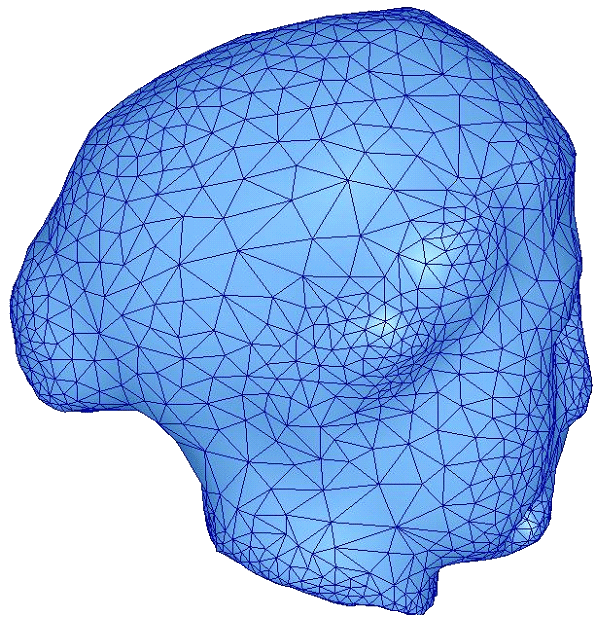
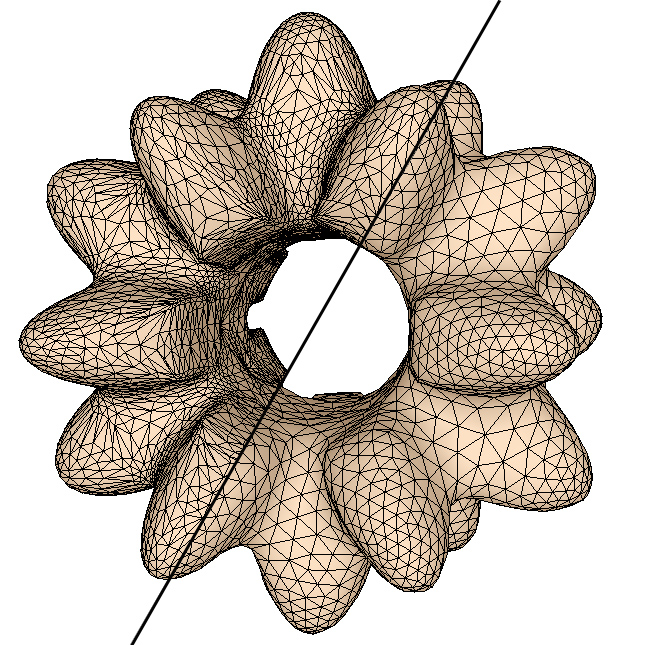
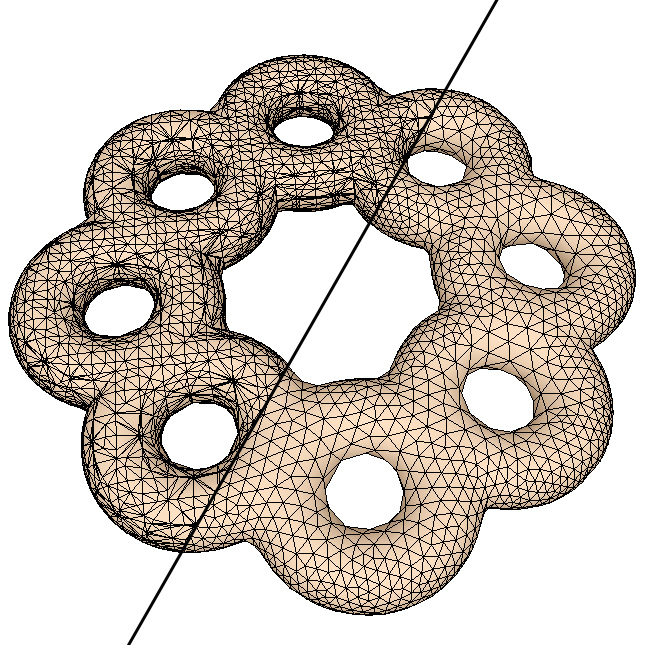
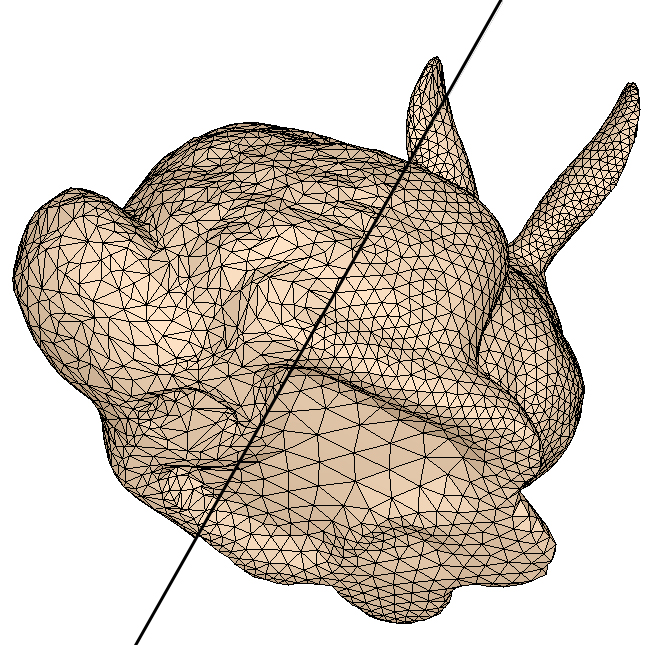
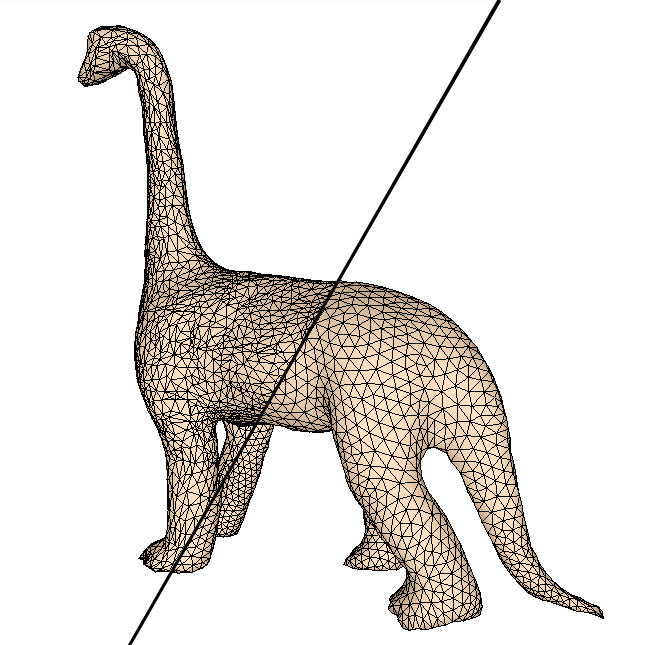
得到离散采样点后，再通过网格重构和优化算法，将可以得到在顶点密度分布、几何拓扑性质上都具有更高质量的重建三维网格模型。对于不同的应用，网格重建的质量的衡量尺度涉及顶点分布、数量、光滑度、三角形的形状、规则性、对原始特征的保持等若干方面。优化的三维网格模型对后续的研究和应用，如网格的编辑、变形、压缩、层次细节等，都将起到非常重要的作用。

▲ 对原始三角网格模型进行顶点重采样以及网格重建，得到的优化三角网格模型

相关论文：

• 付妍,朱晓明,周秉锋, “基于圆形参数域和重要性采样的网格重建”,计算机学报, 30(12):2124 - 2131, 2007年12月.     Download paper

• Yan Fu and Bingfeng Zhou, “Direct Sampling on Surfaces for High Quality Remeshing”, The 2008 ACM symposium on Solid and physical modeling (SPM '08), pp. 115-124, June 2-4, 2008, New York, USA.     Download paper      Download slides

• 付妍，宋本聪，周秉锋, "闭合三角网格的优化切割与保角映射",计算机图形学和辅助设计学报, 20(1):13-18, 2008年1月.     Download paper

• 付妍,“流形三角网格的表面重采样及其应用”，北京大学博士学位论文，2008年6月. Download paper